No $((n,K,d<127))$ Code Can Violate the Quantum Hamming Bound
Abstract
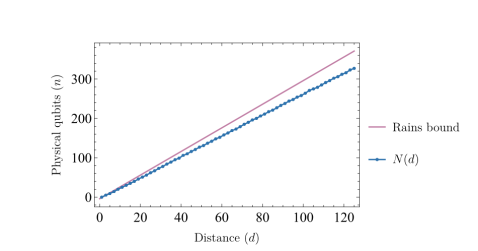
It is well-known that nondegenerate quantum error correcting codes (QECCs) are constrained by a quantum version of the Hamming bound. Whether degenerate codes also obey such a bound, however, remains a long-standing question with practical implications for the efficacy of QECCs. We employ a combination of previously derived bounds on QECCs to demonstrate that a subset of all codes must obey the quantum Hamming bound. Specifically, we combine an analytical bound due to Rains with a numerical bound due to Li and Xing to show that no $((n,K,d))((n,K,d))$ code with $d<127d<127$ can violate the quantum Hamming bound.