Conservation Laws and Quantum Error Correction: Toward a Generalized Matching Decoder
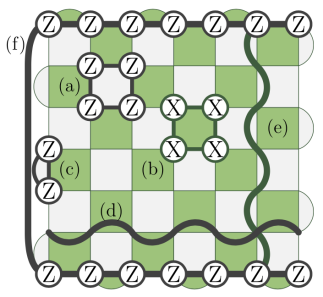
Decoding algorithms are essential to fault-tolerant quantum-computing architectures. In this perspective we explore decoding algorithms for the surface code; a prototypical quantum low-density parity-check code that underlies many of the leading efforts to demonstrate scalable quantum computing. Central to our discussion is the minimum-weight perfect-matching decoder. The decoder works by exploiting underlying structure that arises due to materialized symmetries among surface-code stabilizer elements. By concentrating on these symmetries, we begin to address the question of how a minimum-weight perfect-matching decoder might be generalized for other families of codes. We approach this question first by investigating examples of matching decoders for other codes. These include decoding algorithms that have been specialized to correct for noise models that demonstrate a particular structure or bias with respect to certain codes. In addition to this, we propose a systematic way of constructing a minimum-weight perfect-matching decoder for codes with certain characteristic properties. The properties we make use of are common among topological codes. We discuss the broader applicability of the proposal, and we suggest some questions we can address that may show us how to design a generalized matching decoder for arbitrary stabilizer codes.









